1.直接插入排序
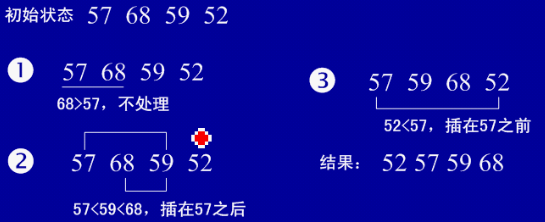
基本思想:在要排序的一组数中,假设前面(n-1) [n>=2] 个数已经是排好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数也是排好顺序的。如此反复循环,直到全部排好顺序。
/**
* 形象描述:踢馆
* 直接插入排序(从小到大)
* @param src 待排序的数组
*/
public void straight_insertion_sort(int[] src){
int tmp;
for (int i = 0; i < src.length; i++) {
tmp = src[i];
int j = i - 1;
//向前匹配,凡是比自己大的都往后移一位,碰到不比自己大的直接跳出
for (; j >= 0 && tmp<src[j] ; j--) {
src[j+1] = src[j];
}
//j-1位置匹配失败,在后一位插入
src[j+1] = tmp;
}
}
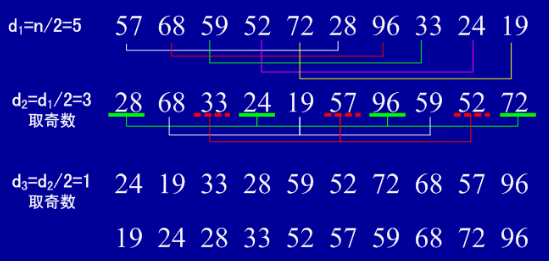
2.希尔排序(缩小增量排序)
基本思想:算法先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差d.对每组中相同位置的元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,再对每组中相同位置的元素进行直接插入排序。当增量减到1时,进行直接插入排序后,排序完成。
/**
* 希尔排序(缩小增量排序)(从小到大)
* @param src
*/
public void shell_sort(int[] src){
int inc = src.length;
int tmp;
while(true){
inc = (int)Math.ceil(inc/2);//增量,亦即每组长度
//遍历每组进行排序的元素索引,具体看内部注释
for (int x = 0; x < inc; x++) {
//以下内容即插入排序,但是搜索头步进inc,回顾时步退inc
//这是一个模拟,可以想象为:将src分组,每组长度为inc,然后对每组的第0,1,2,3...个元素分别进行插入排序
//即:第二组的第一个元素与第一组的第一个元素进行插入排序,第三组的第一个元素与第一二组的第一个元素进行插入排序...
// 第二组的第二个元素与第一组的第二个元素进行插入排序,第三组的第二个元素与第一二组的第二个元素进行插入排序...
// ...
for (int i = x + inc; i < src.length; i += inc) {
tmp = src[i];
int j = i - inc;
for (; j >= 0 && tmp < src[j]; j-=inc) {
src[j + inc] = src[j];
}
src[j + inc] = tmp;
}
}
//不必担心增量为1时会完全等同于普通的直接插入排序,进而造成性能问题
//原因:在排序过程中匹配时遵循"小者胜,大者让"的原则,因此在搜索头进行回顾匹配时,会很快(1~2个元素左右)碰上不久前刚刚打败过自己的对手.
if(inc == 1){
break;
}
}
}
3.简单选择排序
基本思想:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。

/**
* 简单选择排序(从小到大)
* @param src
*/
public void select_sort(int[] src){
int pos,tmp,j; //定义最小值索引,最小值缓存,最小值检索起点索引
//在每个i位置放入合适的值:i==0时放最小值;i==1时放第二小的值...
for (int i = 0; i < src.length; i++) {
//假定i位置的值就是合适的值
tmp = src[i];
pos = i;
//检索i之后的所有元素(前面的元素都比i位置的小),找到一个最小的,与i位置的元素换位
for (j = i+1; j < src.length; j++) {
if(src[j] < tmp){
tmp = src[j];
pos = j;
}
}
src[pos] = src[i];
src[i] = tmp;
}
}
4.堆排序
基本思想:构建一个大顶堆完全二叉树,此时整个二叉树是无序的,二叉树中的无序部分称为堆,堆顶为最大值。将堆中的末尾节点与堆顶节点互换,将刚换到末尾的节点踢出堆(刚被换到末尾的节点与之前被换到末尾的节点之间将是有序的),调整剩余节点,使其满足大顶堆的要求。以此类堆,最后堆将消失,得到一组正序排列的节点。
建堆:
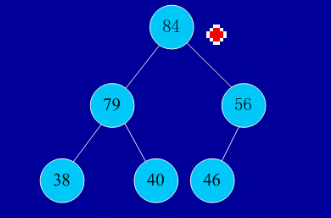
交换,从堆中踢出最大数
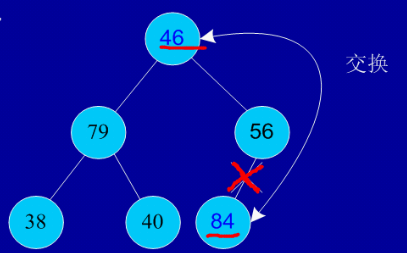
剩余结点再建堆,再交换踢出最大数
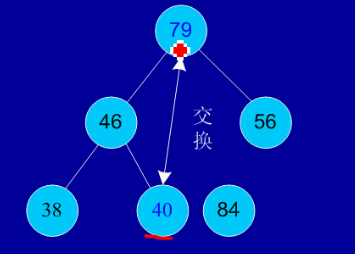
/**
* 调整堆
* @param src 存放节点的数组,节点号从1开始
* @param i 调整起点节点号
* @param size 有效节点长度
*/
private void adjHeap(int[] src,int i,int size){
int lc = 2*i;//左子节点号
int rc = 2*i + 1;//右子节点号
int mx = i;//最大值节点号
//非叶节点最大序号为size/2
if(i<=size/2){
//如果左子节点存在,且大于最大节点
if(lc<=size && src[lc-1]>src[mx-1]){
mx = lc;
}
//如果右子节点存在,且大于最大节点
if(rc<=size && src[rc-1]>src[mx-1]){
mx = rc;
}
//表示节点关系需要变化
if(mx!=i){
swap(src,mx,i);
adjHeap(src,mx,size);
}
}
}
/**
* 交换节点
* @param src 存放节点的数组,节点号从1开始
* @param p 前一个节点号
* @param n 后一个节点号
*/
private void swap(int[] src,int p, int n){
int tmp = src[p-1];
src[p-1] = src[n-1];
src[n-1] = tmp;
}
/**
* 创建初始堆
* @param src 存放节点的数组,节点号从1开始
* @param size 有效节点长度
*/
private void buildHeap(int[] src, int size){
for(int i=size/2; i>=1; i--){
adjHeap(src,i,size);
}
}
/**
* 最大堆排序(从小到大)
* @param src
*/
public void heap_sort(int[] src){
int size = src.length;
buildHeap(src,size);
for(int i=size; i>=1; i--){
swap(src,1,i);
adjHeap(src,1,i-1);
}
}
5.冒泡排序
基本思想:在要排序的一组数中,对当前还未排好序的范围内的全部数,由始至终对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。

/**
* 冒泡排序(从小到大)
* @param src
*/
public void bubble_sort(int[] src){
int tmp;
//移动测头
for (int i = 0; i < src.length; i++) {
//从测头向前推进,若相邻元素前者大于后者,则两者换位
for (int j = i; j > 0; j--) {
if(src[j] < src[j-1]){
tmp = src[j];
src[j] = src[j-1];
src[j-1] = tmp;
}
}
}
}
6.快速排序
基本思想:选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。

/**
* 快速排序(从小到大)
* @param src
*/
public void quick_sort(int[] src){
doSort(src,0,src.length-1);
}
/**
* @param src 数组对象
* @param bi 有效位开头
* @param ei 有效位结尾
* @return
*/
private int getMiddle(int[] src, int bi, int ei){
//缓存开头的元素作为中轴
int tmp = src[bi];
while(bi < ei){
//从右向左开始对比,不比中轴小的元素跳过,并继续向左推进
while(bi < ei && src[ei] >= tmp){
ei--;
}
//能够执行到这里,表示src[ei]<tmp,那么ei位元素应该被放到tmp元素左边,
//但是tmp左边可能有多个元素,该放在什么位置暂时未知,先放在低于tmp的元素区的开头即bi位
//bi位元素已缓存为tmp,不会丢失
src[bi] = src[ei];
//从左向右开始对比,不比中轴大的元素跳过,并继续向右推进
while(bi < ei && src[bi] <= tmp){
bi++;
}
//原理同上,ei位元素在之前已经复制到bi位,ei位已经没有意义了
src[ei] = src[bi];
}
src[bi] = tmp;
return bi;
}
/**
* @param src 数组对象
* @param bi 有效位开头
* @param ei 有效位结尾
*/
private void doSort(int[] src, int bi, int ei){
if(bi >= ei) return;
int mid = getMiddle(src,bi,ei);
doSort(src,bi,mid-1);
doSort(src,mid+1,ei);
}
7.归并排序
基本思想:归并排序法是将两个以上有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列

/**
* @param src 数组对象
* @param bi 有效位开头
* @param ei 有效位结尾
*/
private void doSort(int[] src, int bi, int ei){
if(bi >= ei) return;
int mid = (bi + ei)/2;
doSort(src, bi, mid);
doSort(src, mid + 1, ei);
merge(src, bi, mid, ei);
}
/**
* @param src 数组对象
* @param bi 有效位开头
* @param mid 有效位中点
* @param ei 有效位结尾
*/
private void merge(int[] src, int bi, int mid, int ei){
int[] tmp = new int[ei-bi+1];
int ti = 0; //tmp数组的索引
int fbi = bi; //前半段的起点
int bbi = mid + 1;//后半段的起点
while (fbi<=mid&&bbi<=ei) {
if(src[fbi] <= src[bbi]){
//更小的元素将先被放入tmp,然后再对比下一个
//因为是递归方法,所以前半段是有序的,后半段也是有序的,
//所以前半段的第一个元素比后半段的第一个元素小,那么前半段的第一个元素一定是最小的
//比较大小往tmp中插入的过程其实类似选择排序+希尔排序
tmp[ti++] = src[fbi++];
}else{
tmp[ti++] = src[bbi++];
}
}
//有序元素放入tmp后,前半段的游标可能没有到头(因为后半段的可能先到头了)
while (fbi<=mid){
tmp[ti++] = src[fbi++];
}
//有序元素放入tmp后,后半段的游标可能没有到头(因为前半段的可能先到头了)
while (bbi<=ei){
tmp[ti++] = src[bbi++];
}
//用tmp中排好序的元素替换掉src中指定范围的元素
for (ti = 0; ti < tmp.length; ti++) {
src[bi+ti] = tmp[ti];
}
}
public void merge_sort(int[] src){
doSort(src,0,src.length-1);
}
8.基数排序
基本思想:创建0-9十个容器,对数组中每个数取其相同位的数字,将数组元素放入到对应的容器中,然后按容器顺序从容器中取出放回数组,以此类推当位数递增到最大数的位宽时,排序完成
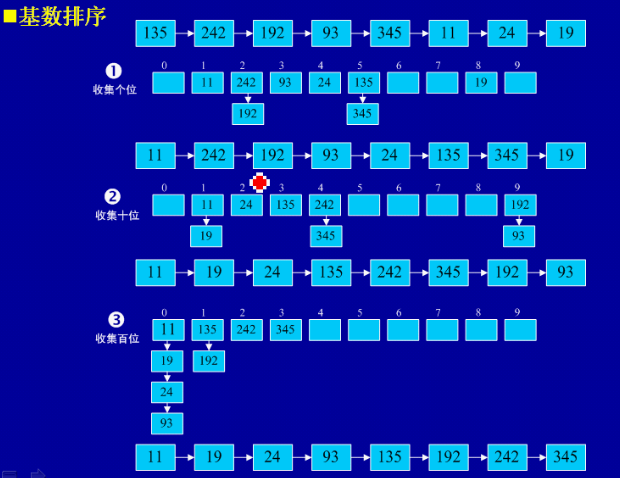
public void radix_sort(int[] src){
//取最大值
int max = src[0];
for (int i = 0; i < src.length; i++) {
max = src[i] > max ? src[i] : max;
}
//取最大值的位数
int w = 0;
while (max>0){
max/=10;
w++;
}
//创建十个队列,用二维数组模拟
int[][] bkt = new int[10][src.length];
//记录每个bkt队列中有几个src元素
int[] cm = new int[10];
for (int i = 0; i < w; i++) {
//遍历元素,按元素的第i位数值分类排放
for (int j = 0; j < src.length; j++) {
int item = src[j];
//求src中第j(从0开始)个元素的第i(从0开始)位数字
//例如987的第1位数字是(987%100)/10
int l = (item % (int)Math.pow(10,i+1))/(int)Math.pow(10,i);
//bkt第l个队列可能有多个数据,用现有的数量表示位置
bkt[l][cm[l]] = item;
//位置后移1位
cm[l] += 1;
}
//重新取出放回src
//记录已经取出的个数
int count = 0;
for (int j = 0; j < 10; j++) {
//第i位为j的元素的个数
int cml = cm[j];
while (cm[j] > 0){
//j从小到大递增,这样取数据将使src具有递增趋势
//将这样的元素存入bkt,将使bkt中每个队列都具有递增趋势
//为了不破换这样的趋势,将需要从每个bkt队列的开头开始取数据
src[count] = bkt[j][cml-cm[j]];
//减去一个元素
cm[j] -= 1;
count++;
}
}
}
}